Put accumulator theta, like digital put strip theta, describes the change in the fair value of a put accumulator due to a change in time to expiry. It is the first derivative of the put accumulator fair value with respect to a change in time to expiry. It is depicted as:
where P is the put accumulator fair value and t is time to expiry.
Evaluating Put Accumulator Theta
Put Accumulator Theta = R1 x Digital Put Theta(K1) + R2 x Digital Put Theta(K2)
+ R3 x Digital Put Theta(K3) + R4 x Digital Put Theta(K4)
where the terms are the digital put options theta with strikes K1, K2, K3 & K4 respectively.
Strikes K1 < K2 < K3 < K4
The payouts in the below examples are:
R1 = 40%, R2 = 30%, R3 = 20% and R4 = 10%
Put Accumulator Theta Over Time
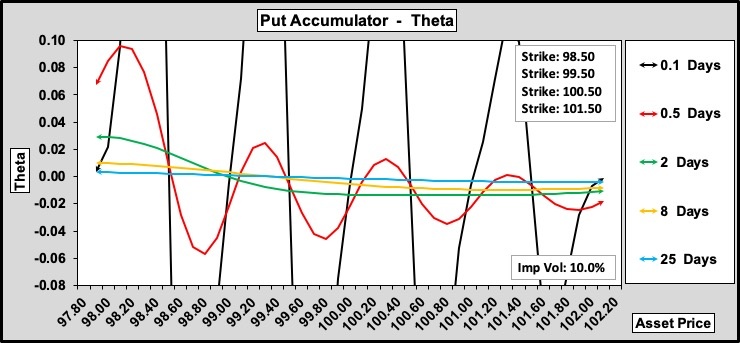
In Figure 1. the black 0.05-day profile shows the theta increasingly rising and plunging around zero as the increasing payouts take effect. With 25-day to expiry the profile is almost flat. The averaging of all four strike’s digital put thetas smooths the manner in which the fair value decays and appreciates.
| European Digitals | Put Accumulator | Put Accumulator Delta | Put Accumulator Gamma | Put Accumulator Vega |
Put Accumulator Theta and Volatility
Here is the put accumulator theta against volatility. Far from being the profile that creates confusion with its oscillations, the theta is now most benign. The theta is almost flat at zero apart from the slope upwards either side of the lowest strike.
As the asset price rises the four theta profiles (apart from the 4%) uniformly descend to a negative reading. They are moving in tandem as the high 25 days to expiry has taken away the ‘get rick quick’ label.
When volatility is trading at 7% and above then selling this put accumulator when the underlying is in the region of 101.00 and premium is high, i.e. 16%, then theta will kick in. Conversely buying the put accumulator with volatility at 16% and asset price at 98.00 also works. Other trades executed with the view of taking in premium are probably not worth the risk of an adverse underlying asset move.