Tunnel gamma is the metric that describes the change in the delta of a tunnel option due to a change in the underlying price. It is the second derivative of the tunnel and first derivative of the tunnel delta with respect to a change in underlying price. It is depicted as:
where 
is gamma and 
is the tunnel delta.
Tunnel Gamma Over Time
Options gamma is crucial in risk management and the tunnel gamma is no different. Figure 1 illustrates the tunnel gamma over a range of time to expiry.
The blue 25-day and 8-day profiles are pretty flat which is no surprise since those respective profiles of Figure 1 of tunnel delta are also flat.
The 2-day profile is negative between the strikes and positive outside the strikes.
The 0.5 and 0.1 days to expiry gamma profiles provide such switchback ride it would be pointless even attempting sustainable risk management.
The point about digital options is that, unlike conventional options, the writer has limited loss. This advantage is only accorded the conventional optional buyer as the short conventional call writer has potential unlimited losses. The limited risk nature of digital options often throw up these gyrating risk metrics. Yet they are probably only of interest to wholesale FX traders since for retail, digitals always offer capped risk trading.
| European Digitals | Tunnel Options | Tunnel Delta | Tunnel Theta | Tunnel Vega |
Tunnel Option Gamma and Volatility
Figure 2 shows more dramatic gamma profiles…….
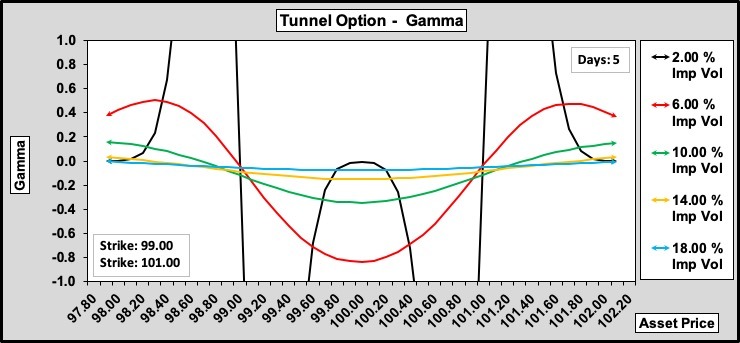
…..but the scale shows even less risk. The gamma scale (-1.0 to +1.0) encompasses all profiles (except for the unrealistic 2.0%) which suggests minimum exposure to changes in volatility.
Summary
The volatile nature of the tunnel gamma would suggest that maybe, possibly quite rightly, it is more trouble than it’s worth. Certainly the way the gamma whips between negative and positive leaves little scope for action. This Tunnel Greek is of more relevance when absorbed into a portfolio of other options based on the underlying asset. Otherwise best to keep it as a read-only adjunct to active management.